Histogramme
- Overview, Purpose &, Key Terms
- History & Background
- Creating a Histogram
- Interpretation
- Example
- Software
- Related Topics
Overview
Overview: This histogram tutorial will provide information on how to construct and
interpret histograms for use in quality process control (Q.C.). The main areas that will
be covered in this tutorial are the following:
- Tutorial Instructions
- Histogram Background
- Creating a Histogram (interactively by example)
- Interpreting Histograms
- Recommended Additional Q.C. Topics and Software
Purpose: The purpose of this tutorial is to let you become familiar with graphical histograms which are used widely in quality control (Q.C.). Histograms are effective Q.C. tools which are used in the analysis of data. They are used as a check on specific process parameters to determine where the greatest amount of variation occurs in the process, or to determine if process specifications are exceeded. This statistical method does not prove that a process is in a state of control. Nonetheless, histograms alone have been used to solve many problems in quality control.
- Key Terms:
- Histogram -
- a vertical bar chart of a frequency distribution of data
- Q.C. Methodology -
- a statistical tool used in the analysis and determination of possible solutions to quality control problems in industry
- Frequency Distribution -
- a variation in a numeric sample of data
| HISTORY | CONSTRUCTION | INTERPRETATIONS | EXAMPLE | SOFTWARE | RELATED TOPICS |
History & Background
The histogram evolved to meet the need for evaluating data that occurs at a certain frequency. This is possible because the histogram allows for a concise portrayal of information in a bar graph format.
The histogram is a powerful engineering tool when routinely and intelligently used. The histogram clearly portrays information on location, spread, and shape that enables the user to perceive subtleties regarding the functioning of the physical process that is generating the data. It can also help suggest both the nature of, and possible improvements for, the physical mechanisms at work in the process.
| OVERVIEW | CONSTRUCTION | INTERPRETATIONS | EXAMPLE | SOFTWARE | RELATED TOPICS |
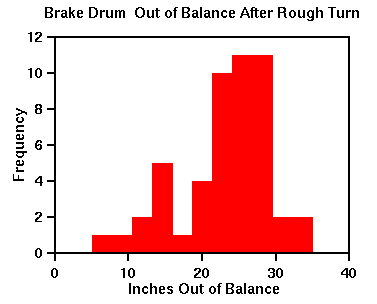
Creating a Histogram
- Determine the range of the data by subtracting the smallest observed measurement from
the largest and designate it as R.
Example: Largest observed measurement = 1.1185 inches Smallest observed measurement = 1.1030 inches R = 1.1185 inches - 1.1030 inches =.0155 inch
- Record the measurement unit (MU) used. This is usually controlled by the measuring
instrument least count.
Example: MU = .0001 inch
- Determine the number of classes and the class width. The number of classes, k, should be
no lower than six and no higher than fifteen for practical purposes. Trial and error may
be done to achieve the best distribution for analysis.
Example: k=8
- Determine the class width (H) by dividing the range, R, by the preferred number of
classes, k.
Example: R/k = .0155/8 = .0019375 inch The class width selected should be an odd-numbered multiple of the measurement unit, MU. This value should be close to the H value: MU = .0001 inch Class width = .0019 inch or .0021 inch
- Establish the class midpoints and class limits. The first class midpoint should be
located near the largest observed measurement. If possible, it should also be a convenient
increment. Always make the class widths equal in size, and express the class limits in
terms which are one-half unit beyond the accuracy of the original measurement unit. This
avoids plotting an observed measurement on a class limit.
Example: First class midpoint = 1.1185 inches, and the class width is .0019 inch. Therefore, limits would be 1.1185 + or - .0019/2.
- Determine the axes for the graph. The frequency scale on the vertical axis should slightly exceed the largest class frequency, and the measurement scale along the horizontal axis should be at regular intervals which are independent of the class width. (See example below steps.)
- Draw the graph. Mark off the classes, and draw rectangles with heights corresponding to the measurement frequencies in that class.
- Title the histogram. Give an overall title and identify each axis.
Now you have a histogram!!
| OVERVIEW | HISTORY | INTERPRETATIONS | EXAMPLE | SOFTWARE | RELATED TOPICS |
Interpretations
When combined with the concept of the normal curve and the knowledge of a particular process, the histogram becomes an effective, practical working tool in the early stages of data analysis. A histogram may be interpreted by asking three questions:
- Is the process performing within specification limits?
- Does the process seem to exhibit wide variation?
- If action needs to be taken on the process, what action is appropriate?
The answer to these three questions lies in analyzing three characteristics of the histogram.
- How well is the histogram centered? The centering of the data provides information on the process aim about some mean or nominal value.
- How wide is the histogram? Looking at histogram width defines the variability of the process about the aim.
- What is the shape of the histogram? Remember that the data is expected to form a normal or bell-shaped curve. Any significant change or anomaly usually indicates that there is something going on in the process which is causing the quality problem.
Examples of Typical Distributions
NORMAL
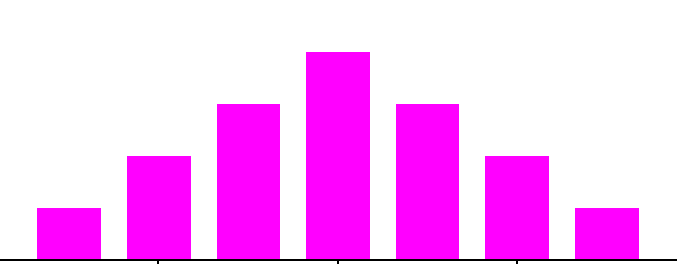
- Depicted by a bell-shaped curve
- most frequent measurement appears as center of distribution
- less frequent measurements taper gradually at both ends of distribution
- Indicates that a process is running normally (only common causes are present).
BI-MODAL
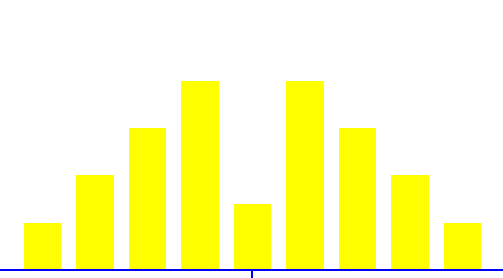
- Distribution appears to have two peaks
- May indicate that data from more than process are mixed together
- materials may come from two separate vendors
- samples may have come from two separate machines.
CLIFF-LIKE
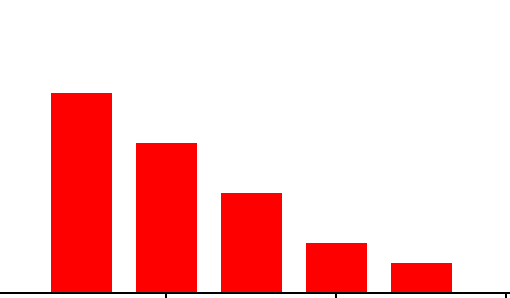
- Appears to end sharply or abruptly at one end
- Indicates possible sorting or inspection of non-conforming parts.
SAW-TOOTHED
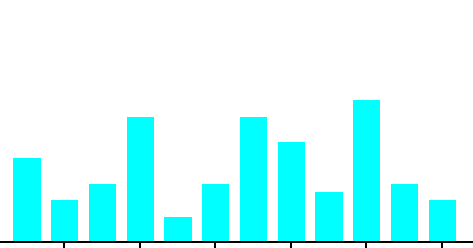
- Also commonly referred to as a comb distribution, appears as an alternating jagged pattern
- Often indicates a measuring problem
- improper gage readings
- gage not sensitive enough for readings.
SKEWED
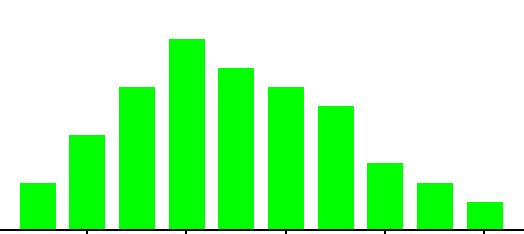
- Appears as an uneven curve; values seem to taper to one side.
It is worth mentioning again that this or any other phase of histogram analysis must be married to knowledge of the process being studied to have any real value. Knowledge of the data analysis itself does not provide sufficient insight into the quality problem.
- OTHER CONSIDERATIONS
- Number of samples.
- For the histogram to be representative of the true process behavior, as a general rule, at least fifty (50) samples should be measured.
- Limitations of technique.
- Histograms are limited in their use due to the random order in which samples are taken and lack of information about the state of control of the process. Because samples are gathered without regard to order, the time-dependent or time-related trends in the process are not captured. So, what may appear to be the central tendency of the data may be deceiving. With respect to process statistical control, the histogram gives no indication whether the process was operating at its best when the data was collected. This lack of information on process control may lead to incorrect conclusions being drawn and, hence, inappropriate decisions being made. Still, with these considerations in mind, the histogram's simplicity of construction and ease of use make it an invaluable tool in the elementary stages of data analysis.
| OVERVIEW | HISTORY | CONSTRUCTION | EXAMPLE | SOFTWARE | RELATED TOPICS |
Example
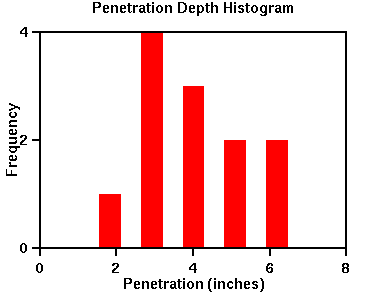
The following example shows data collected from an experiment measuring pellet penetration
depth from a pellet gun in inches and the corresponding histogram:
Penetration depth (inches) __________________________ 2 3 3 3 3 4 4 4 5 5 6 6
Some important things to remember when constructing a histogram:
- Use intervals of equal length.
- Show the entire vertical axes beginning with zero.
- Do not break either axis.
- Keep a uniform scale across the axis.
- Center the histogram bars at the midpoint of the intervals (in this case, the penetration depth intervals).
| OVERVIEW | HISTORY | CONSTRUCTION | INTERPRETATIONS | SOFTWARE | RELATED TOPICS |
Software
- Evaluation of Histogramming Packages
- P. Ganev, S. Hellman, R. Jones . Table of Contents . 1.0 Introduction . 2.0 Evaluation of the histogramming packages . 2.1 PAW . 2.1.1 General description of the package. . 2.1.2 Description of data formats required...
- Computer Software Development
- Software Development Projects . The Common Histogram Object . Show: An Implementation of the Common Histogram Object . 3D Data Visualization . mail-feedback . Last Modified: Dec 24 1994
- pnmhisteq(1) USER COMMANDS pnmhisteq(1)
- NAME pnmhisteq - histogram equalise a portable anymap SYNOPSIS pnmhisteq [-gray] [-rmap pgmfile] [-wmap pgmfile] [-verbose] [pnmfile] DESCRIPTION pnmhisteq increases the contrast of a portable graymap or pixmap through the technique of histogram ...
- E852 Data Processing
- Production analyzer
| OVERVIEW | HISTORY | CONSTRUCTION | INTERPRETATIONS | EXAMPLE | RELATED TOPICS |
Related Topics
- Frequency histogram
- Bell shape
- Skewed distribution
- Uniform distribution
- Bimodal distribution
- Truncated distribution
| OVERVIEW | HISTORY | CONSTRUCTION | INTERPRETATIONS | EXAMPLE | SOFTWARE |